一、神经网络的基本概念
1. 神经元(感知器)
一种被称为感知器的人工神经元在20世纪五六十年代被科学家Frank提出。通过数学模型,可以认识到感知器是一个根据输入与权重来做出决定的设备,随着权重和阈值的变化,可以得到不同的决策模型。当一个感知器计算后得到的值大于阈值时,从神经学的角度来讲这个感知器被激活,反之为0。感知器可以一定程度上模仿人脑做出决策,但是感知器的决策过程全部是线性的,在处理图像处理、语音识别等复杂问题时,难以仅靠线性模型达到良好的识别效果,因此需要在感知器模型种引入非线性部分。
2. 非线性神经元
为解决复杂的数学模型,引入激活函数,激活函数给神经元带来了非线性因素,使得神经网络可以任意逼近任何非线性函数。
通常将激活函数与线性神经元合并使之成为非线性神经元
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。
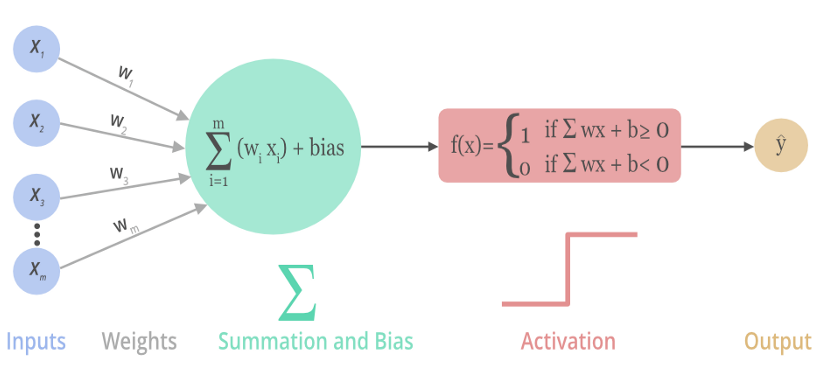
激活函数可以分为两大类:

- 饱和激活函数: sigmoid、 tanh…
- 非饱和激活函数: ReLU 、Leaky Relu 、ELU、PReLU、RReLU…
深度学习中常见的10种激活函数(Activation Function)总结_激活函数有哪些-CSDN博客
3.常见的激活函数
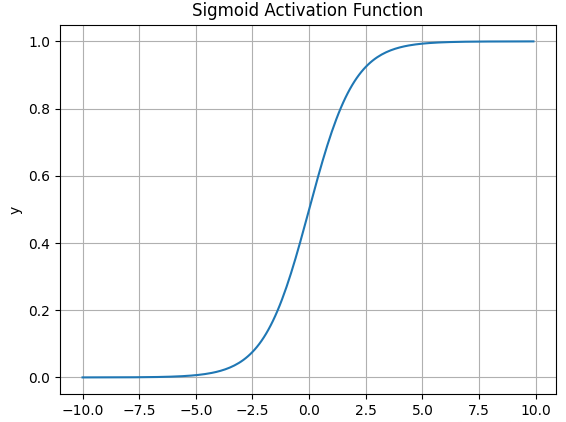
3.1 Sigmoid函数
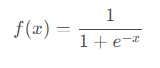
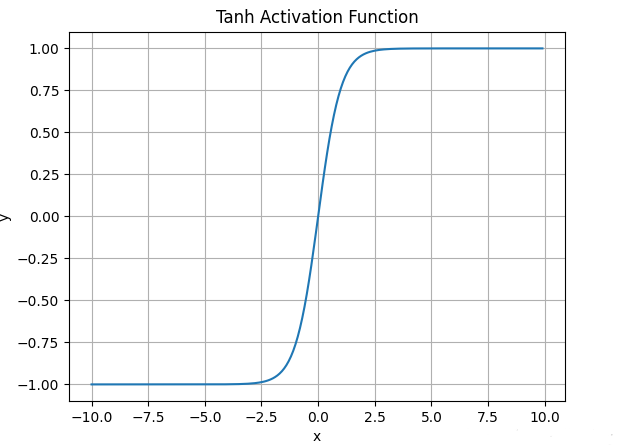
3.2 tanh函数
tanh激活函数的数学表达式为:
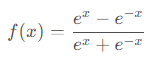
函数图像如下:
3.3 ReLU函数
ReLU激活函数的数学表达式为:
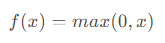
函数图像如下:
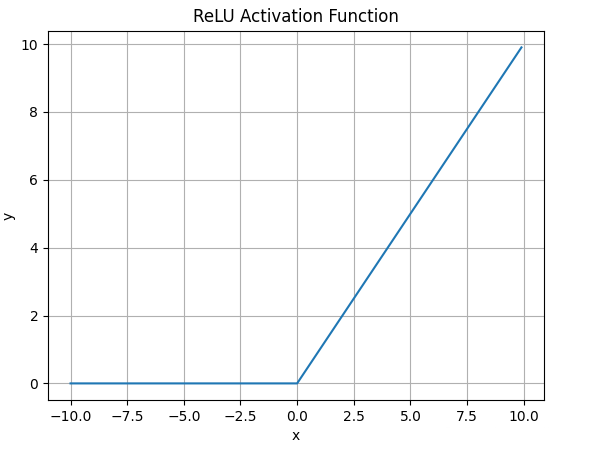
什么情况下适合使用ReLU?
-
ReLU解决了梯度消失的问题,当输入值为正时,神经元不会饱和
-
由于ReLU线性、非饱和的性质,在SGD中能够快速收敛
-
计算复杂度低,不需要进行指数运算
ReLU有哪些缺点?
-
与Sigmoid一样,其输出不是以0为中心的
-
Dead ReLU 问题。当输入为负时,梯度为0。这个神经元及之后的神经元梯度永远为0,不再对任何数据有所响应,导致相应参数永远不会被更新
-
训练神经网络的时候,一旦学习率没有设置好,第一次更新权重的时候,输入是负值,那么这个含有ReLU的神经节点就会死亡,再也不会被激活。所以,要设置一个合适的较小的学习率,来降低这种情况的发生
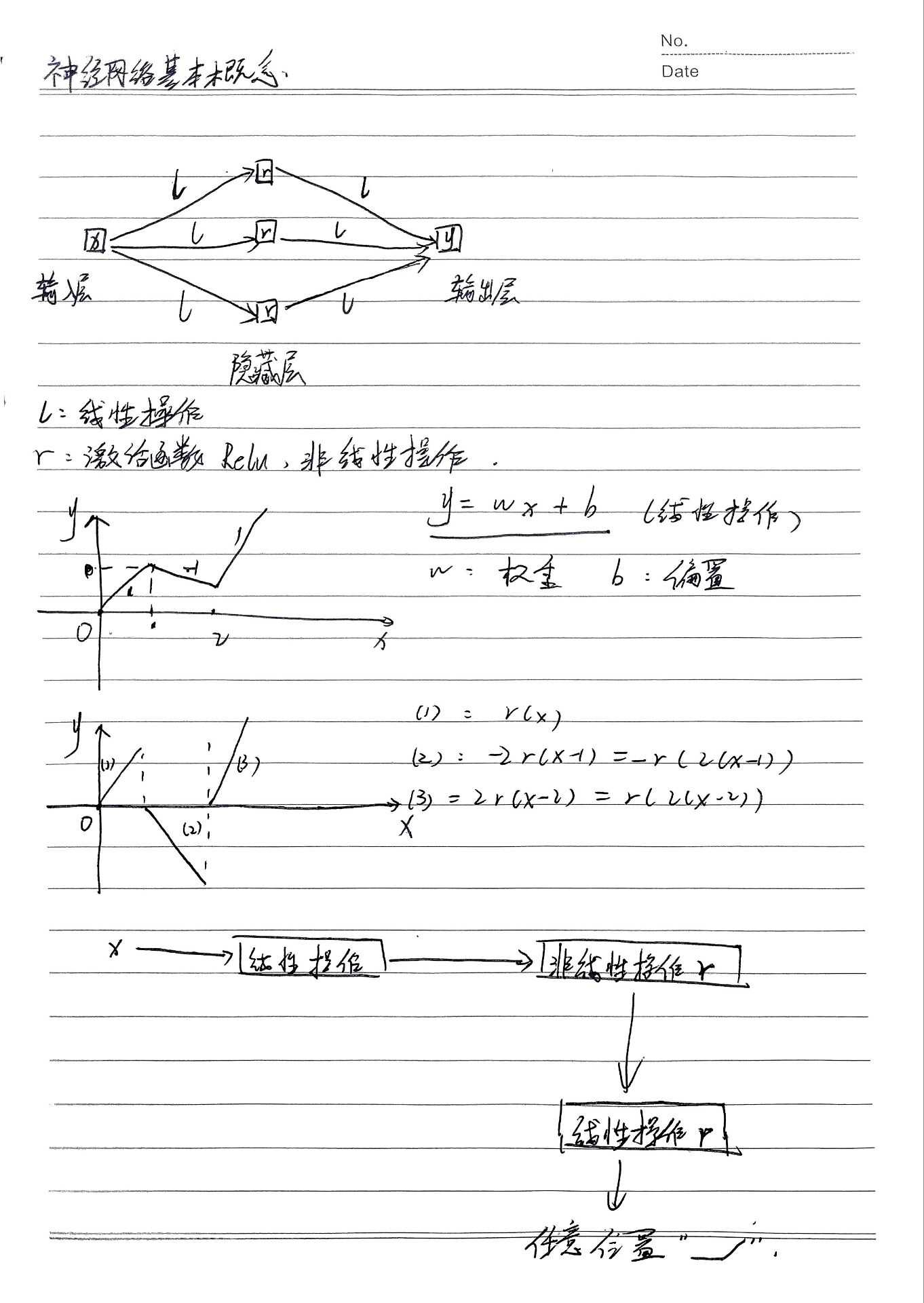
4. 神经网络的基本架构
-
神经网络最左边的称为输入层,其中的神经元称为输入神经元,原始数据经由该层输入到神经网络进行后续处理。
-
最右边的称为输出层,包含输出神经元,该层的输出是神经网络对样本处理后的最终结果,如分类结果。
-
在输入层和输出层之间的是中间层,也称为 隐藏层,即既非输入也非输出的神经网络层,一个神经网络可以有一个或者多个隐藏层,隐藏层的主要作用是处理从上一层神经元传递来的信号。
一般的,输入层和 输出层在整体神经网络的外部,称为可见层。设计神经网络的输入输出通常比较简单,直接,例如,假设我们知道了一朵花的4个明显特征(如花瓣的长度,宽度),可以利用这4个特征确定它是哪一种类的花,由于我们已经知道这朵花的4个特征,那么就需要4个输入神经元,每个数值代表花朵的一种特征的具体数值。输出层可以包含一个或者多个神经元,这由我们想要设定的具体花朵类别决定,可以根据输出的数字,确定花朵的类型。我们可以使用每一个输出神经元代表一种类型的花,这种方法称为One-Hot,One-Hot是一种常见的输出层编码方法。
5. 梯度下降
机器学习-梯度下降算法原理及公式推导_梯度下降计算公式-CSDN博客
6. 反向传播
“反向传播算法”过程及公式推导(超直观好懂的Backpropagation)_反向传播算法(过程及公式推导)-CSDN博客
“正向传播”求损失,“反向传播”回传误差。同时,神经网络每层的每个神经元都可以根据误差信号修正每层的权重
思考
一、输入x是 784长度的向量,什么机制使得输出y变成的长度为10的向量?
将长度为784的向量 xx 转换为长度为10的向量,是通过全连接层(Fully Connected Layer) 实现的。具体操作通过 权重矩阵 和 偏置向量 来完成。
1. 全连接层的基本机制:
全连接层的工作机制可以用矩阵乘法来描述。给定输入向量 xx(长度为784),要转换为长度为10的输出向量,通常通过如下步骤:
2. 步骤:
-
输入向量
:这是一个长度为784的向量,表示神经网络的输入。
-
权重矩阵
:全连接层会有一个权重矩阵 WW,其维度是 10×78410×784,表示从输入784维向量到输出10维向量的权重连接。每一行表示一个输出神经元与所有输入神经元的权重连接。
-
偏置向量
:偏置向量 bb 是一个长度为10的向量,表示每个输出神经元的偏置。
-
计算输出向量
:通过矩阵乘法计算输出向量。输出向量 oo 的维度是10。具体计算方式如下:
- W \cdot x ):矩阵 ( W ) 乘以向量 ( x ),将784维的输入向量映射为10维的输出向量。
3. 矩阵乘法具体步骤:
-
假设输入向量
是长度为784的向量:
-
权重矩阵 WW 是一个 10×78410×784 的矩阵:
-
偏置向量 bb 是一个长度为10的向量:
-
输出向量 oo 通过矩阵乘法和加法得到,维度为10:
每一行表示一个输出神经元的结果,最终得到一个长度为10的向量。
4. 激活函数:
在得到长度为10的向量后,通常会将其通过激活函数进行处理。在分类任务中,输出层通常使用 Softmax 函数,将每个输出值转换为概率值。Softmax 函数公式为:
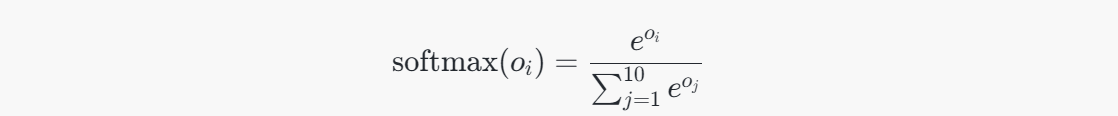
这会将输出向量 oo 转换为一个概率分布,表示输入属于不同类别的概率。
总结:
将784长度的输入向量变为10长度的输出向量的关键步骤是通过 全连接层的矩阵乘法 和 偏置项,最终计算出长度为10的向量,并通过 Softmax 函数将其转换为概率分布,从而实现分类。
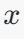 :这是一个长度为784的向量,表示神经网络的输入。
:这是一个长度为784的向量,表示神经网络的输入。
 :全连接层会有一个权重矩阵 WW,其维度是 10×78410×784,表示从输入784维向量到输出10维向量的权重连接。每一行表示一个输出神经元与所有输入神经元的权重连接。
:全连接层会有一个权重矩阵 WW,其维度是 10×78410×784,表示从输入784维向量到输出10维向量的权重连接。每一行表示一个输出神经元与所有输入神经元的权重连接。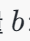 :偏置向量 bb 是一个长度为10的向量,表示每个输出神经元的偏置。
:偏置向量 bb 是一个长度为10的向量,表示每个输出神经元的偏置。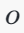 :通过矩阵乘法计算输出向量。输出向量 oo 的维度是10。具体计算方式如下:
:通过矩阵乘法计算输出向量。输出向量 oo 的维度是10。具体计算方式如下: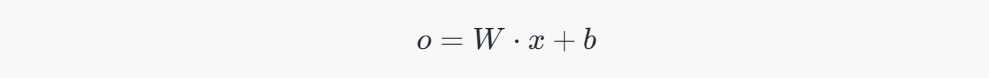





![【stm32单片机】[操作系统][RT-Thread][3]线程通信](/img/blog_cover/rt-thread.jpg)